南京师范大学附属中学新城初级中学(210019) 宋远征
题目 如图1,在∆ABC中,AB=AC,∠BAC=α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE,DE.
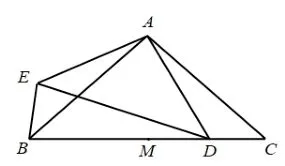
图1
(1)比较∠BAE与∠CAD的大小; 用等式表示线段BE,BM,MD之间的数量关系,并证明;
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
文献[1]和[2]从不同的角度进行探究与思考,特别是运用同一法,将条件与结论互换,从结论出发,倒推出垂直,再根据基本事实“过直线外一点有且只有一条直线与已知直线垂直”证明唯一性,转换了思考的角度,拓宽了解决问题的空间.
图形的平移变换改变的是线段的位置,不变的是特定的数量关系和特殊的位置关系,如果将ED平移到合适的位置,将问题进行合适的转换,从将研究的重心从N点转移到M点上,从而降低了研究的难度.从角平分线的角度出发,引导学生尝试构造倍半角的模型,如图2,延长EB到G使得BG=BD,连接DG,易知DG//AB,过N作NQ⊥MN交BC于P点,则NQ//AB,交EG于Q点,若EN=ND,可得Q是EG的中点且PM=BE=CD.但是这个思路是依据N为ED的中点倒推出来的,若根据Q为EG中点,连接QN,却较难证明QN⊥EM,以及N为ED的中点,因此考虑从证明PM=BE来寻找突破.

图2
思路1将线段ED沿着NM方向平移到GH,如果N是ED的中点,则M点是GH的中点.
方法1如图3,过E作EG⊥AB,垂足为G点,过D作DQ⊥AB,垂足为Q,过C作CH⊥DQ交QD的延长线于H点,连接MG、MH.下证G、M、H三点是共线的.由作图易知AB//CH,所以∠3=∠2.由第(1)问可知∠1=∠2,所以∠1=∠3.又因为∠EGB=∠DHC=90◦和BE=CD,可证∆BEG∆CDH(AAS),所以BG=CH,EG=DH.再由已知得BM=CM,结合∠3=∠2 和BG=CH可证∆BGM∆CHM(SAS),所以GM=HM,∠GMB=∠HMC,所以∠GMB+∠GMC=∠HMC+∠GMC=180◦,则G、M、H三点共线.由EG⊥AB和MN⊥AB,可得EG//MN,又因为GM=HM,根据平行线分线段成比例可证EN=ND.

图3
方法2运用同一法.如图3,过E作EG⊥AB,垂足为G点,过D作DQ⊥AB,垂足为Q,过C作CH⊥DQ交QD的延长线于H点,连接GH,设BC和GH的交点为M′.
同解法1,可证明∆BEG∆CDH(AAS),所以BG=CH.由BG=CH,∠GMB=∠CMH,∠3=∠2,可证∆BGM′∆CHM′(AAS),可得BM′=CM′,即M′为BC的中点,因此M′与M重合.
剩下步骤同解法1.
反思将探究的目标通过图形的变换转换到合适的位置进一步的探讨,降低分析的难度.在方法1 最后部分,帮助学生巩固平行线分线段成比例定理在证明题中的运用.
思路2构造“一线三等角”通过计算来证明线段长度相等.
方法3如图4,过N点作NP⊥MN,交BC于P点,连接AN、AM.因为PN⊥MN,AB⊥MN,所以PN//AB,可知∠3=∠2.易知∠4=∠3=∠C,根据“一线三等角”易证∆PND∽∆CDA,则设AM=1,MD=a,MC=b,MP=x,则
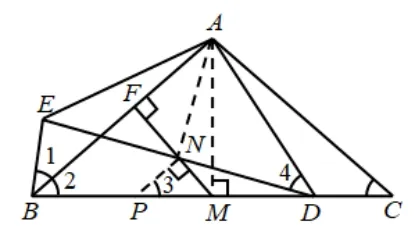
图4
因为AB=AC,M为BC的中点,所以AM⊥MC,即∠AMC=∠MPN=90◦,又因为∠3=∠C,可证∆MPN∽∆ACM,则即所以PN=由知解得x=b−a,即PM=CD.由和PM=CD,知又因为∠3=∠4,得∆AND∽∆MNP,所以∠MNP=∠AND=90◦.又因为AE=AD,根据“三线合一”得N为ED的中点.
方法4如图5,过N点作NP⊥MN,交BC于P点,方法3 证明了PM=CD.在MN的延长线上截取NQ=NM,连接NQ、EQ.可知NP为MQ的垂直平分线,则PQ=PM,且∠QPN=∠MPN,易知∠QPM=∠EBM,所以EB//PQ,又因为EB=CD=PM,所以EB=PQ,即四边形EBPQ为平行四边形,则EQ=PB=MD,且EQ//PB.易证∆EQN∆DMN,则NE=ND.

图5
方法5如图2,过N点作NP⊥MN,交BC于P点,根据方法3 有PM=CD=EB.过D作DG//AB交EB的延长线于G点,延长NP与EG交于Q点.所以有∠G=∠1,∠3=∠2,则∠G=∠3,得BG=BD,同理可证BQ=BP,则QG=PD=BM.因为EQ=EB+BQ=PM+BP=BM,所以EQ=QG,根据平行线分线段成比例得EN=ND.
方法6如图6,过N点作NP⊥MN,交BC于P点,过E作AB的平行线交CB的延长线于G点,由∠1=∠3,∠2=∠G,可证GB=BE,由方法3 知PM=CD=EB,因为BM=CM,则可证PD=GP,又因为PN//AB,利用平行线分线段成比例得ND=NE.

图6
反思思路2 中的核心条件是PM=BE且PM⊥MN,要使得两个条件同时满足,通过作图是无法直接实现的,因此需要借助计算的手段来进一步判断,计算过程中借助“一线三等角”寻找相似,再通过比例关系的计算来证明PM=BE.
思路3如图7,以M为原点建立平面直角坐标系,通过计算证明N为ED中点.
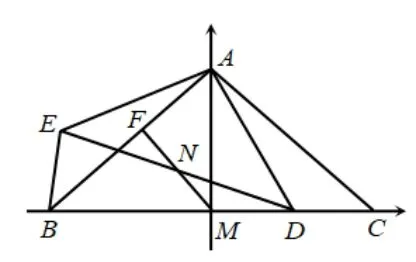
图7
方法7设A(0,1),B(b,0),D(a,0),E(m,n),可求出DE所在直线的函数表达式为y=(m−a).同理可得kAB=因为AB⊥MN,则kMN=b,则MN所在直线的函数表达式为y=bx.联立方程组可求出F点坐标为由EA=AD知m2+(n−1)2=12+a2,化简得m2+n2=2n+a2,由EB=CD知(m−b)2+n2=12+(−b−a)2,化简得m2+n2=2mb+2ab+a2.联立上述两个式子得n=(m+a)b,所以根据中点坐标公式,F点为ED的中点.
方法8运用同一法,取DE的中点N′,根据方法7 中的设法,则N′的坐标为,由方法6 知n=(m+a)b,kMN′=则kMN′kAB=所以MN′⊥AB,由于过M点有且只有一条直线与AB垂直,因此MN与MN′是重合的,即N与N′重合,N′为DE的中点.
反思一次函数中,斜率乘积为−1 的两条直线互相垂直,对于初中阶段的学生来说可以借助“一线三垂直”构造相似,运用代数推理进行证明,因此这个结论对于学有余力的学生来说并不难理解,建立直角坐标系,运用数形结合的方法解决问题的好处就是尽可能的不用辅助线,可以作为拓展学生思维的一种方法.
4.1 整理基本构图方法,总结图形结构特征
对学生来说,复杂的几何图形往往让他们无法快速找到解题思路,引导和鼓励学生整理常见的构图方法,总结图形的结构特征,能够有效地促进学生探索解决问题的方向.特别是通过构造“一线三等角”模型,运用计算来证明线段相等的方法,在以往的练习中,与学生讨论过这样的一道习题:
如图8,在正方形ABCD中,M是BC边上任意一点,P是BC延长线上一点,N是∠DCP平分线上一点,若∠AMN=90◦,求证:AM=MN.

图8
批改学生的作业发现,绝大部分学生首先想到的是作NG⊥BP构造“一线三垂直”,在证明∆ABM和∆MNG全等时,没有对应的边相等,好像这条路被堵住了,但是在构图的过程中发现,如果M点位置确定,N点的位置是唯一确定的,其中一定隐藏着线段之间的数量关系,反过来倒推条件,我们要证明的结论AM=MN一定是成立的,必有∆ABM∆MGN,便有BC=MG,即BM=CG=NG,借助“一线三等角”得∆ABM∽∆MGN,则有设AB=1,BM=x,MC=1−x,CG=GN=a,即解得x=a,即BM=CG.我们将这个例子中学习的经验,运用到了本题中的思路2 中,证得MP=CD后,根据“三线合一”、“角平分线+等腰+平行”或者“倍半角”等基本的构图方法,寻找解题的突破口.
4.2 加强运算能力训练,在试错中勇敢前行
在运用数形结合的方法时,与学生一起讨论的过程中,一开始的各种尝试并不是很顺利,需要引入字母参数来表示点的坐标或者直线的函数表达式,如果设的字母个数较少或者较多,对于某些线段或者点坐标的代数表达式就会非常的复杂,对后续的计算产生心理上障碍,例如只设两个参数表示出C、D点的坐标,利用∠ABC的三角函数值构造二倍角的图形结构求出∠EBC的三角函数值,从而表示E点的坐标,但是由于数据过于复杂,后续的运算则无法进行下去.关于运算素养的培养,不仅仅是为了追求计算的结果,更重要的是面对综合性较强的问题上,需要总结如何将复杂的运算变得简便、高效.对于思路4,合理的设置了4 个参数,避免不必要的计算过程,只需要恰当的表示出关键的条件EA=AD且EB=CD,通过消去高次元的方式得到4 个参数之间的数量关系,就运用代数推理推导出中点表达式或者计算k值乘积为−1.
解题的过程就是一种历练,特别是面对复杂的代数式计算时,不仅是考察学生的运算素养,更是心理素质的训练,面对错误也不放弃尝试,勇敢前行,在成功解决问题的过程中感受数学解题带来的成就感.
猜你喜欢延长线平行线中点例谈圆锥曲线中的中点和对称问题中学生数理化(高中版.高考数学)(2021年4期)2021-07-20平行线故事作文·低年级(2021年4期)2021-05-06南京地铁二号线既有线与延长线的施工及转场组织研究科学家(2021年24期)2021-04-252020年本刊原创题(二)初中生学习指导·中考版(2020年4期)2020-09-10中点的联想学苑创造·C版(2018年3期)2018-05-28添加平行线 求角真方便中学生数理化·七年级数学人教版(2017年2期)2017-03-25“平行线及其判定”检测题中学生数理化·七年级数学人教版(2017年1期)2017-03-25不可思议的平行线初中生世界·七年级(2017年1期)2017-01-20准PR控制的三电平逆变器及中点平衡策略电测与仪表(2016年5期)2016-04-22带续流开关的中点箝位型非隔离光伏逆变器电测与仪表(2016年17期)2016-04-11






